Two Proportions

Two Proportions

---

Remember that the normal distribution can be used to approximate the binomial distribution in certain cases. Specifically, the approximation was considered good when np and nq were both at least 5. Well, now, we're talking about two proportions, so np and nq must be at least 5 for both samples.
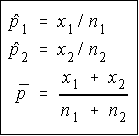We don't have a way to specifically test two proportions for values, what we have is the ability to test the difference between the proportions. So, much like the test for two means from independent populations, we will be looking at the difference of the proportions.
We will also be computing an average proportion and calling it p-bar. It is the total number of successes divided by the total number of trials. The definitions which are necessary are shown to the right.
The test statistic has the same general pattern as before (observed minus expected divided by standard error). The test statistic used here is similar to that for a single population proportion, except the difference of proportions are used instead of a single proportion, and the value of p-bar is used instead of p in the standard error portion.
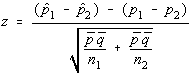Since we're using the normal approximation to the binomial, the difference of proportions has a normal distribution. The test statistic is given.
Some people will be tempted to try to simplify the denominator of this test statistic incorrectly. It can be simplified, but the correct simplification is not to simply place the product of p-bar and q-bar over the sum of the n's. Remember that to add fractions, you must have a common denominator, that is why this simplification is incorrect.
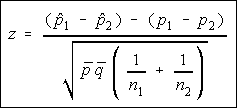The correct simplification would be to factor a p-bar and q-bar out of the two expressions. This is usually the formula given, because it is easier to calculate, but I wanted to give it the other way first so you could compare it to the other formulas and see how similar they all are.
Okay, someone might see a slight problem here. We're supposed to be testing to see if the two proportions are equal. We have no idea what they're equal to, just that they're equal to each other. So, what values do we put in for p₁ and p₂?

All hypothesis testing is done under the assumption that the null hypothesis is true.

Well, if the null hypothesis is true, then the two proportions are equal to each other, and the difference between them is zero. So, it doesn't matter what they might be, we just need to know that the difference is zero.